汉诺塔问题是一个经典的问题,涉及将一堆盘子从一个柱子移动到另一个柱子,并遵守特定的规则,例如,不能将大盘子放在小盘子上面。汉诺塔问题可以使用递归算法解决。
递归算法的思想是将大问题分解为小问题,再通过小问题的解决方案来解决大问题。对于汉诺塔问题,递归算法的步骤如下:
- 如果只有一个盘子,直接将盘子从起点柱子移动到目的柱子。
- 如果有多个盘子,需要将盘子分成两部分:最上面的盘子和其他盘子。
- 先将其他盘子从起点柱子移动到中间柱子,使用递归算法。
- 再将最上面的盘子从起点柱子移动到目的柱子。
- 最后,将其他盘子从中间柱子移动到目的柱子,使用递归算法。
递归算法的核心是递归,即重复调用自身来解决小问题,直到问题的规模足够小,可以直接使用基本情况的解决方案。递归算法在汉诺塔问题中是非常有效的,因为它可以将大问题分解为小问题,再由小问题的解决方案得出大问题的解决方案。递归算法的代码实现也很简单,可以使用任何编程语言实现。
递归算法的一个问题是它容易导致栈溢出,因为每次递归都会创建新的函数调用栈帧。如果递归深度过大,则可能导致栈溢出,从而终止程序的执行。为了避免栈溢出,可以使用迭代算法,例如非递归算法。
总的来说,汉诺塔递归算法是一种简单易懂、高效的解决方案,是学习递归算法的一个好的入门问题。
以下是汉诺塔问题的几个示例程序:
- Python代码:
def hanoi(n, src, dst, mid):
if n == 1:
print("Move disk 1 from rod", src, "to rod", dst)
return
hanoi(n - 1, src, mid, dst)
print("Move disk", n, "from rod", src, "to rod", dst)
hanoi(n - 1, mid, dst, src)
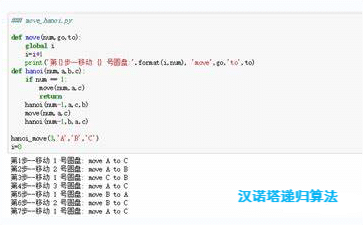
hanoi(3, 'A', 'C', 'B')
- Java代码:
class Hanoi {
public static void main(String[] args) {
hanoi(3, 'A', 'C', 'B');
}
public static void hanoi(int n, char src, char dst, char mid) {
if (n == 1) {
System.out.println("Move disk 1 from " + src + " to " + dst);
return;
}
hanoi(n - 1, src, mid, dst);
System.out.println("Move disk " + n + " from " + src + " to " + dst);
hanoi(n - 1, mid, dst, src);
}
}
- C++代码:
#include <iostream>
using namespace std;
void hanoi(int n, char src, char dst, char mid) {
if (n == 1) {
cout << "Move disk 1 from " << src << " to " << dst << endl;
return;
}
hanoi(n - 1, src, mid, dst);
cout << "Move disk " << n << " from " << src << " to " << dst << endl;
hanoi(n - 1, mid, dst, src);
}
int main() {
hanoi(3, 'A', 'C', 'B');
return 0;
}
这些代码都可以帮助您更好地理解汉诺塔递归算法。
关于TeamDoc软件:
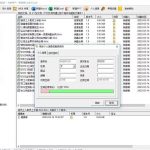
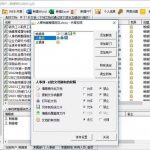
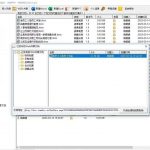
TeamDoc是基于服务器/客户端架构的轻量级文件管理软件。TeamDoc将文件集中加密存储在您单位自己的服务器中,员工使用TeamDoc客户端访问服务器,从而获得与自己权限相关的权限:登入后与“我的电脑”界面类似,可以看到自己该看的文件,编辑自己能编辑的文档,对于能看到的文件,还可以细分文档权限,进而做到能看不能拷,能看不能截屏等功能,多种权限灵活设置,在线协同编辑、全文搜索、日志与版本追踪,快速构建企业文档库。告别假大空,我们提供值得您选择的、易用的、可用的文档管理软件。现在就访问TeamDoc首页
TeamDoc软件界面(点击可放大)
版权所有:南京网亚计算机有限公司,本文链接地址: 汉诺塔递归算法代码简洁例程